深度学习介绍¶
终于来到了激动人心的章节!深度学习这个词,不需要过多的解释,大家都已经耳熟能详了,从2006年到现在,尤其是AlphaGo的延生,让深度学习在整个星球上热了起来。这个Note将给大家介绍这门技术。
1. 深度学习的沉浮¶
Deep Learning如此的火热,吸引了全世球那么多人的注意力,DeepLearning正在引领多个领域的变革,它不是一个靠吹捧出来的技术,而是实实在在的渗透到各个应用上。下面我们从2012年到2016年Google内部用于Deep Learning技术的项目的个数变化曲线。
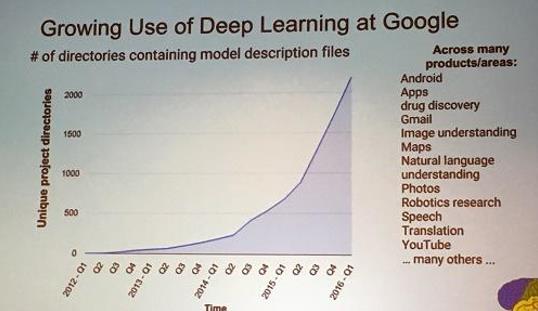
从图上可以看出来,Deep Learning的应用正在成指数型的增长。
但如果回头来看DeepLearning的整个发展历程来看,并不是一帆风顺的,虽然Deep Learning这个词是2006年左右被定义出来,但它的相关技术早在60年代就发展出来了。
- 1958: Perceptron (linear model)
- 1969: Perceptron has limitation:只能处理线性可分的问题,没有激活单元
- 1980s: Multi-layer perceptron :Do not have significant difference from DNN today
- 1986: Backpropagation: Usually more than 3 hidden layers is not helpful
- 1989: 1 hidden layer is “good enough”, why deep?,这个质疑让多层感知机失去了发展动力
- 2006: RBM initialization
- 2009: GPU
- 2011: Start to be popular in speech recognition
- 2012: win ILSVRC image competition
- 2015.2: Image recognition surpassing human-level performance
- 2016.3: Alpha GO beats Lee Sedol
- 2016.10: Speech recognition system as good as humans
2. 用深度学习解决问题的三个步骤:¶
2.1 定义模型的数学表达形式¶
让我们用之前定义的机器学习的三个步骤来学习深度学习,看一下深度学习在这三个方面是如何做的。
在上一个note的最后部分,我们定义了一种级联的logstic regression结构,而且也说到了这种结构就是deep learning的结构。确实如此!
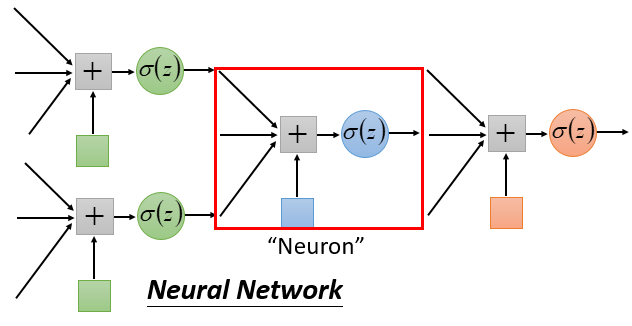
深度学习中的网络结构我们称之为:“神经网络”(Neural Network)。它就由一个个logistic regression单元(这里我们称之为神经元Neuron)来组成的一个图结构。
我们可以定义不同的图结构来形成不同类型的神经网络,常听说的有:DNN、CNN、RNN等。它们都是因为神经元之间联结方式不同而形成的。一旦我们选择好了一个神经网络的结构,实际上我们就定义好了一个Function Set。
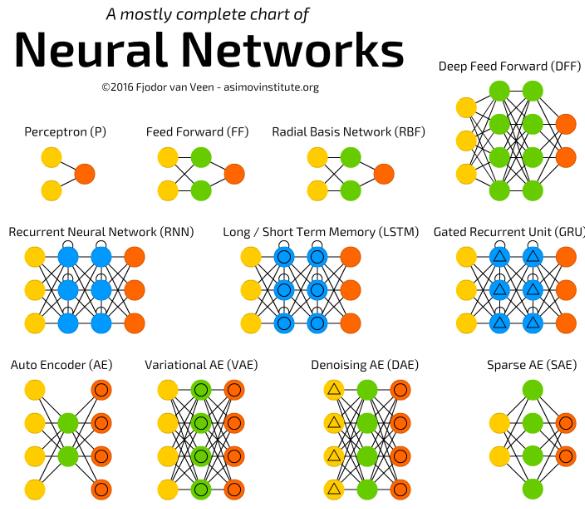
我们先从最简单的神经网络结构开始:Fully Connect Feedforward Network。
全连结的前馈神经网络从组成上来说分成两种组成部分:神经元与层,其中层是由神经元构成的。层和层按序排列形成一个前馈形的结构。下一层的神经元与上一层的每个神经层通过权重相联。层从功能上划分为三种类型:输入层、隐藏层、输出层。
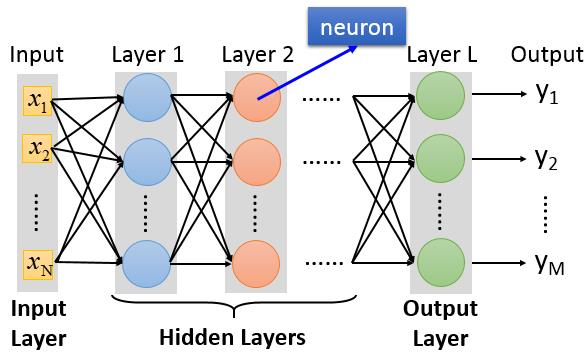
对于Deep Learning来说,实际上就是指Hidden Layers很多。像这两年出来的一些深度学习的网络模型
- AlexNet: 8层
- VGG:19层
- GoogleNet:22层
- ResNet:152层
下面我们来看一下,对于Fully Connected Feedforward Network是如何进行计算的。
我们用$\mathbb{x}$来表示输入向量,$a^l$表示第$l$层隐藏层的输出向量,用$y$来表示最终的输出。而层与层之间是通过权重矩阵进行连结,我们用$W^l,b^l$表示第$l$层与前一层之前的权重参数。
则整神经网络的计算过程为:
$$a^1 = \sigma(W^1x+b^1)$$$$a^2 = \sigma(W^2a^1+b^2)$$$$\cdots$$$$y = a^L = \sigma(W^La^{L-1}+b^L)$$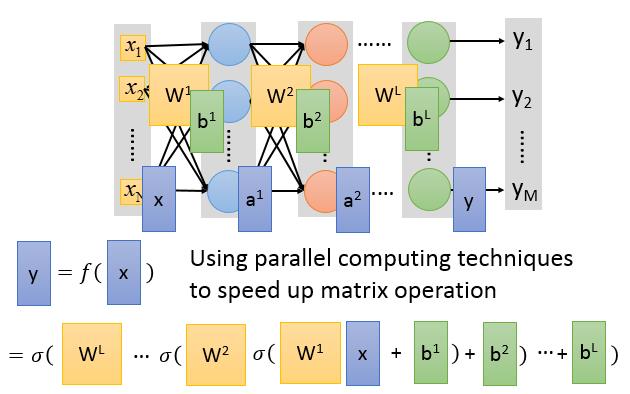
对于上面的结构,它的输出$y$是一个多维的向量,我们可以把整神经网络当作一个特征抽取器,$y$就是我们对于$x$抽取到的特征。如果我们要做分类任务,那我们需要在$y$后面再接一下logistic regression分类器,或SVM分类器。
所以如果我把把神经网络最后一层设计为一个Softmax层,那整个网络就是一个多分类问题的function set了。
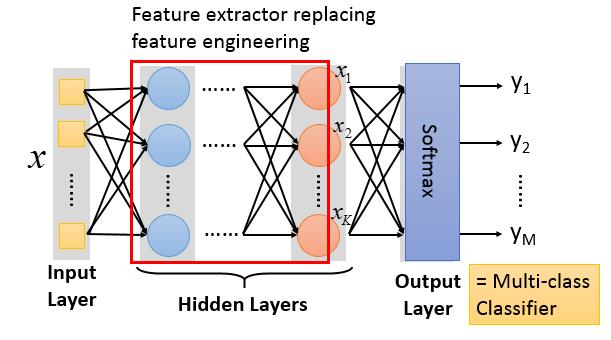
举个例子,如果我们要做手写体识别,那么我们就可以利用上面的网络结构,由于我们的数字手写体识体的样本是16×16的图片,所以整个网络的输入是一个256维的向量,输出是一个10*1的向量。
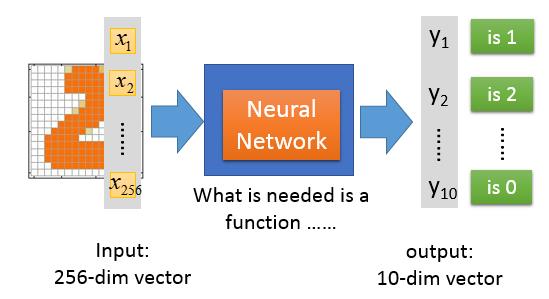
但当们设计好输入、输出后,对于整个网络内部该是什么样子的我们确没有明显的设计指导,隐藏层用多少层,每一个隐藏层该有多少个神经元,这些都是固定的范式的。需要反复试验和一些直觉来完成。
2.2 神经网络的评价¶
怎么去评价我们选择的神经网络参数的好坏呢,当然是从输出结果上来看,拿分类任务来说,我们最终选择是Softmax作为我们的输出层,输出的是输入属于每一类的概率,所以像在Logistic Regression回归中,我们可以选择多分类的交叉熵作为我们的损失函数。
$$L(f) = \sum_{n-1}^N l^n$$$$l(y,\hat{y}) = -\sum_{i=1}^{10}\hat{y_i}\ln y_i$$2.3 选择最好的模型参数¶
来到了我们解决机器学习问题的第三步,有了function set,有了评价function的函数,如何找到最合适的function呢。
Gradient Descent!
我们的优化目标是:
$${W^1}^*,{b^{1}}^*,\cdots,{W^L}^*,{b^{L}}^* = \arg\max_{W,b}L(f)$$所以如何把我们神经网络的参数写为$[w_1,w_2,\cdots,b_1,b_2,\cdots]$,那么我们用梯度下降算法求解问题,最终就是计算:
$$\nabla L = [\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \cdots, \frac{\partial L}{\partial b_1}, \frac{\partial L}{\partial b_2},\cdots]$$然后我们对神经网络的参数进行迭代更新:
$$\theta' = \theta - \eta\nabla L$$那如何计算$\nabla L$呢,由于DeepLearning的发展,出现了很多深度学习的框架,它们提供了一些机制可以让我们不用手动的计算$\nabla L$,提供了极大的方便。著名的有:TensorFlow, Caffe2, PyTorch,MXNet等。我们通过下面的一个小节简要说明是如何利用反向传播计算$\nabla L$的。
3. 反向传播¶
学习Backprogation前,我们先复习一下微积分里的链式法则(Chain rule)。
对于$y = g(x), z = h(y)$这样的复合函数,$z$对$x$的导数为
$$\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}$$而对于$x = g(s), y = h(s), z = k(x,y)$这种多路径的复合函数,$z$对$s$的导数为
$$\frac{dz}{ds} = \frac{dz}{dx}\frac{dx}{ds} + \frac{dz}{dy}\frac{dy}{ds}$$从链式法则中可以看出,如果一个变量的改变是经过中间多个函数的传递导致最终的变化,梯度会沿着计算路径的反方向传递回来。
我们设每个神经元在被激活函数作用之间的结果为$z$,神经元的输出为$a = \sigma(z)$,那么对于第$l$隐藏层的参数$w^l,b^l$来说
$$\frac{\partial L}{\partial w^l_{ij}} = \frac{\partial L}{\partial z^l_i}\frac{\partial z^l_i}{\partial w^l_{ij}}$$其中的$\frac{\partial z^l_i}{\partial w^l_i}$我们是很容易计算出来的
$$\frac{\partial z^l_i}{\partial w^l_{ij}} = a^{l-1}_j$$那$\frac{\partial L}{\partial z^l_i}$ 如何计算呢,每一个$z^l_i$最终会通过下一层的$z^{l+1}$来影响$L$,所以:
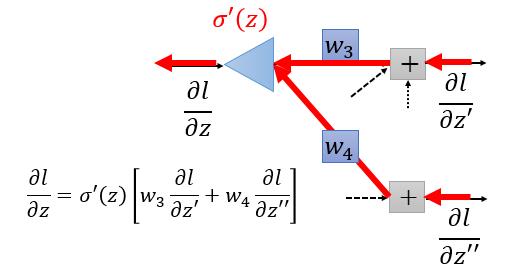
$$\frac{\partial L}{\partial z^l_i} = \sum_k^K \frac{\partial L}{\partial z^{l+1}_k}\frac{\partial z^{l+1}_k}{\partial z_i^l}$$$$\frac{\partial z^{l+1}_k}{\partial z_i^l} = \frac{\partial z^{l+1}_k}{\partial a^l_i}\frac{\partial a^l_i}{\partial z^l_i} = w_{ki}^{l+1}\sigma(z_i^l)(1-\sigma(z_i^l))$$$$\frac{\partial L}{\partial z^l_i} = \sum_k^K \frac{\partial L}{\partial z^{l+1}_k} w_{ki}^{l+1}\sigma(z_i^l)(1-\sigma(z_i^l)) = \sigma(z_i^l)(1-\sigma(z_i^l))\sum_k^K \frac{\partial L}{\partial z^{l+1}_k} w_{ki}^{l+1}$$从下面的推导我们看出要计算$\frac{\partial L}{\partial z^l_i}$,只需要计算$\frac{\partial L}{\partial z^{l+1}_i}$,是一个递归依赖的关系。所以我们只要求出最后一层的$\frac{\partial L}{\partial z^l_i}$,那整个网络的参数的梯度就都求出来了。
同理对于$\frac{\partial L}{\partial b}$也是如此。
所以整个梯度的计算实际是是从网络的后面向前面计算,反射的过程。
4. 总结¶
本节开始正式介绍深度学习的基本结构——神经网络,描述了神经网络的结构组成,和神经网络中组成单元的术语。然后像一般的机器学习模型解决问题一样,我们从三个步骤入门来看如何用神经网络来解决分类问题。最后介绍了神经网络训练的反向传播方法。